Trading facile, archéologie graphique ou mathématiques ingénieuses ? Tout d'abord, vous devriez prendre un moment pour réfléchir à la citation suivante du mathématicien boursier obsessionnel Max Cohen, tirée du grand film "Pi" :

"1. Les mathématiques sont le langage de la nature. 2. Tout ce qui nous entoure peut être représenté et compris par des nombres. 3. Si vous représentez graphiquement les chiffres de n'importe quel système, des modèles émergent. 4. Conclusion : les modèles existent partout dans le monde."

Max Cohen est obsédé par la recherche d'une formule qui lui permettra de prévoir le prix de n'importe quelle action x à la virgule près. Pendant ce temps, il tente de composer avec le chiffre pi, les nombres de Fibonacci, les juifs kabbalistiques et, enfin et surtout, les grandes sociétés de Wall Street qui ont eu vent de sa découverte prochaine. C'est une entreprise ambitieuse que d'être capable de prédire l'ensemble du marché - une bonne histoire de film, après tout - mais les hypothèses de base de Max Cohen peuvent être appliquées de manière tout à fait pratique, comme vous le verrez avec le pattern de Gartley.

La stratégie de puissance du motif de Garley

Motifs de Garley et Fibonacci

Examinons d'abord ce qui suit : La ligne numérique de Fibonacci est l'un des modèles mathématiques les plus récurrents dans la nature. On le retrouve dans la propagation des populations d'essaims ainsi que dans la disposition des graines d'une fleur de tournesol. La série de nombres de Fibonacci peut être décrite très simplement. Chaque élément suivant est la somme des deux précédents : 1, 1, 2, 3, 5, 8, 13, 21, 34, et ainsi de suite.

Cependant, l'aspect le plus important de cette série est que les fractions formées par deux éléments consécutifs (par exemple, 13/21) se rapprochent de ce que l'on appelle le "nombre d'or". Le nombre d'or décrit la "relation harmonieuse" dans laquelle deux longueurs peuvent se trouver l'une par rapport à l'autre : 1.618:1. Le corps humain possède d'innombrables rapports de ce type, par exemple au niveau des articulations des doigts. Mais aussi les coquilles de coquillages ou les rayons de miel des abeilles, voire les galaxies comme notre Voie lactée, sont créés selon le nombre d'or.

L'intérêt principal réside toutefois dans les marchés et les graphiques. Ici, il est également possible d'observer qu'il existe des modèles basés sur le nombre d'or et donc sur la série de nombres de Fibonacci. C'est la raison pour laquelle Max Cohen la suit dans le nombre "Pi". Les retracements de Fibonacci sont un outil populaire dans l'analyse technique car grâce à eux, vous pouvez très rapidement localiser les endroits sur les graphiques où un rapport de 1,618:1 s'est produit. Cela devrait vous être familier. Moins populaire est le fait que, d'autre part, il existe des modèles qui sont créés et fonctionnent selon des ratios de Fibonacci définis.

Origine et histoire

Le motif de Gartley remonte, comme son nom l'indique, à son concepteur H. M. Gartley, qui a décrit sa structure de base dès 1935 dans son livre "Profits in the Stock Market". Avec d'autres modèles exotiques, il est inclus dans le groupe des modèles harmoniques et est considéré comme le plus ancien et le plus connu d'entre eux. Les modèles harmoniques sont des modèles graphiques composés d'une séquence de retracements de Fibonacci aussi exacte que possible.

Il est intéressant de noter qu'à l'époque de la publication de Gartley, le concept de retracements était totalement inconnu et il n'en est pas fait mention explicitement. Par conséquent, les ratios originaux du modèle de Gartley diffèrent légèrement des retracements de Fibonacci exacts qui sont utilisés aujourd'hui.

Définition et structure

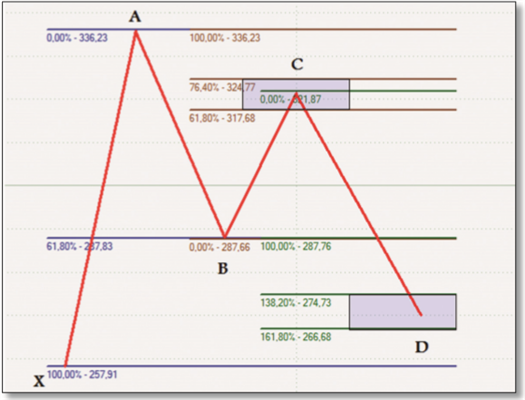
La figure 1 montre un échantillon d'un modèle de Gartley haussier. Après que tout mouvement à la hausse (XA) ait conduit à un sommet, le prix doit d'abord corriger aussi exactement que possible de 61,8 pour cent (AB, bleu). Le contre-mouvement initié ensuite doit à nouveau être une correction dans un rapport d'au moins 61,8 pour cent, au maximum 76,4 pour cent (BC, marron). Cependant, le dernier morceau qui suit (CD, vert) devrait être au moins 161,8 pour cent plus grand que le précédent et devrait clôturer au point D à environ 76,4 pour cent de correction de la hauteur totale du motif (XA). Le point D décrit également l'entrée dans une position longue.  Tout cela peut sembler un peu exotique et confus, mais vous n'aurez aucun problème à le comprendre après l'avoir regardé plusieurs fois. La seule chose nécessaire pour créer un modèle de Gartley est le rapport correct entre les mouvements de prix et les contre-mouvements. Cela signifie que les figures de Gartley peuvent apparaître sur n'importe quel graphique, pour n'importe quel sous-jacent et n'importe quelle période de temps, indépendamment de l'évolution actuelle des prix ou des divers indicateurs techniques.

Figure 1. Modèle de Gartley haussier. Vous pouvez voir ici la structure théorique d'un modèle de Gartley : un mouvement donné corrige 61,8 %, puis 61,8 % à nouveau, puis 161,8 % - pour un total d'environ 76,4 % du mouvement initial.

Simplification et manipulation

C'est une entreprise complexe et longue que de déterminer des modèles de Gartley exactement selon les définitions qui viennent d'être mentionnées, puisqu'il faut créer de nombreuses lignes de Fibonacci, les modèles de Gartley sont difficiles à trouver et il y a encore trop de place pour l'interprétation. Si vous suivez strictement les définitions, alors vous pouvez avoir découvert une belle configuration, cependant, des questions se posent sur l'endroit où entrer en position, où le stop doit être placé, et quand une configuration Gartley est parfaite ou imparfaite. N'oubliez pas que vous êtes un trader, pas un archéologue ! Ainsi, pour une application stratégique holistique du motif Gartley, il est essentiel de résoudre ces questions ouvertes - quelle que soit la qualité de la figure.

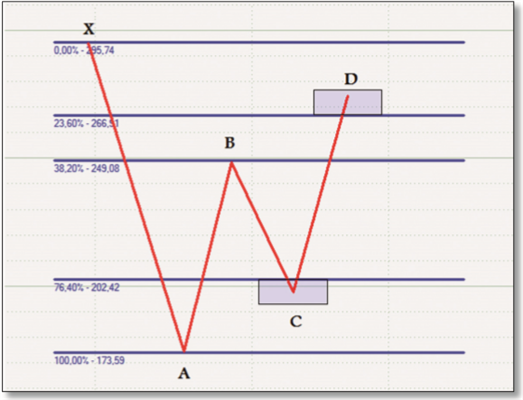
De manière analogue au motif Gartley haussier, il existe un motif Gartley baissier, qui peut être appliqué exactement dans l'autre sens et qui vise les transactions à découvert, comme le montre la figure 2. Vous pouvez voir qu'au lieu de trois comme dans la figure 1, il n'y a qu'un seul retracement de Fibonacci. En fait, cela suffit aussi, car une fois que vous faites le calcul, les retracements de 23,6 % et de 76,4 % sont suffisants pour déterminer l'emplacement des points C et D, respectivement. Exactement : X et A définissent les 100 % complets. B devrait corriger aussi exactement que possible 61,8 pour cent, ce qui signifie courir à 38,2 pour cent. Si un contre-mouvement de 61,8 % a lieu à nouveau au point C, nous nous retrouvons au retracement original de 76,4 %. Disons que 76,4 pour cent est un nombre d'or de second ordre. Comme il existe par définition une légère tolérance pour la position du point C, l'encadré de la figure 2 a pour but de préciser sa position possible. De même, le point D, dont on sait qu'il se situe au-dessus du retracement de 23,6 pour cent, est également mis en évidence comme une zone.

Figure 2 : Modèle de Gartley baissier. L'utilisation de ces modèles baissiers montre que l'illustration simplifiée des modèles rend le trading réel beaucoup plus facile. Le point B est une correction de 61,8 %, les points C et D restent dans des zones autour de 23,6 % et 76,4 %.

Les modèles Gartley expliqués

Les modèles Gartley en pratique

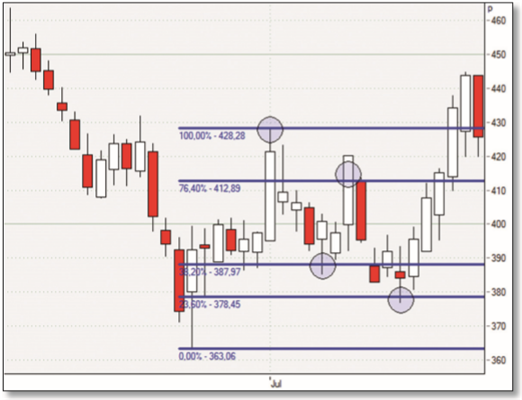
Pour illustrer ces théories approfondies, il convient de se pencher sur un exemple pratique. Dans la figure 3, vous trouverez le graphique journalier de la valeur britannique Tate & Lyle. Sur ce graphique, vous pouvez voir un véritable modèle de Gartley - haussier. Il commence par un mouvement conventionnel à la hausse (premier cercle, 100 %, point A). À partir de ce sommet, le prix corrige presque exactement de 61,8 % (deuxième cercle, 38,2 %, point B). Le prix se retourne et franchit la ligne de retracement supérieure (troisième cercle, 76,4 %, point C). Cependant, le sommet n'est pas atteint et le prix redescend. Avec le franchissement de la ligne de retracement de 23,6 % (quatrième cercle, point D), le modèle de Gartley est entièrement formé. Le point d'entrée idéal se situe à 378,45. Pas de stratégie sans stop : celui-ci se situe à 363,06 (point X, 0 %).

Figure 3. Exemple de Tate & Lyle, graphique quotidien. Ce graphique montre un motif de Gartley haussier qui s'est formé de manière presque parfaite. Le système de trading reconnaît une entrée claire ici. Avec le stop et l'objectif, il est probable de réaliser un profit ici.

Lorsque le point A avec 428,28 est défini comme objectif de prix, cette sortie permet de réaliser un bon profit après seulement cinq jours de conservation. En chiffres : Environ 50 points de profit pour un risque d'environ 15 points. Cette stratégie pourrait être étendue en visant un objectif de prix plus éloigné ou en négociant le breakout au-dessus du point A de manière classique. Le profit créé par la réussite du motif de Gartley pourrait alors servir d'excellent tampon de risque. Comme vous pouvez le constater, il ne s'agit pas d'une stratégie achevée, mais d'une sorte de base qui peut être étendue et systématisée à volonté. Rappelez-vous : "Les schémas existent partout dans le monde". La tâche consiste à les reconnaître et à les mettre en œuvre de manière rentable.

Exemple 2 - Pas de précipitation

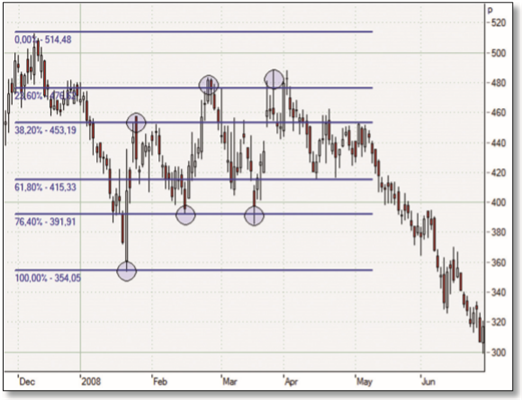
Dans la figure 4, vous pouvez voir un autre exemple du modèle de Gartley, cette fois-ci baissier, dans le graphique de Lloyds TSB, une autre valeur britannique de l'indice FTSE. Si vous observez brièvement ce graphique, il va maintenant s'expliquer de lui-même. Après les quatre premiers cercles brillamment formés (points A, B, C, D), on pouvait en toute confiance entrer en position vendeuse à 476. Il est intéressant de noter que le mouvement C-D s'est répété presque à l'identique. Toutefois, il ne faut pas s'en inquiéter, mais plutôt souligner que les modèles, quels qu'ils soient, ne doivent pas toujours se poursuivre exactement une fois qu'ils ont été formés. Le trading n'est pas une science exacte et les marchés sont toujours lunatiques.

Toutefois, tant que le stop et l'objectif d'entrée sont clairement définis, il n'y a aucune raison de s'agiter - car au final, ce modèle de Gartley a également permis de réaliser un bon bénéfice. Regardez où en est Lloyds TBS aujourd'hui !

Conclusion de la stratégie du motif de Gartley

Il n'est pas poli d'anticiper la fin d'un film, mais pour une fois, il faut faire une exception pour l'illustration finale de cet article.

Max Cohen échoue dans sa tentative, souffre de crises d'épilepsie et finit par retrouver la raison, les firmes de Wall Street repartent les mains vides et, malheureusement, les juifs traditionalistes doivent eux aussi se contenter de rien. Il n'est pas réaliste de prédire avec précision tous les mouvements du marché, quelle que soit la taille de cet ensemble de chiffres et le nombre de modèles que l'on peut y reconnaître. Néanmoins, l'idée de nombres et de modèles est tout à fait appropriée, car le parallélisme de Fibonacci peut être observé dans la nature et dans les graphiques.

Le modèle de Gartley est une preuve de la façon dont on peut faire du profit à partir de modèles uniques. Mais malheureusement, il ne suffit pas d'observer la nature pour faire du profit ; il faut intégrer cette approche dans une stratégie globale. Cela implique de fixer des stops, des objectifs et une gestion cohérente des risques et de l'argent.

N'oubliez pas que vous n'avez pas à prouver ou à prévoir quoi que ce soit avec précision. Après tout, vous êtes un trader, pas un mathématicien ! Source : Traders' Mag.

A lire également

• Détecter les configurations graphiques.
• L'automatisation des niveaux de Fibonacci.